Cost-category product(1)
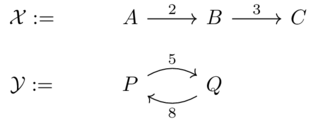
Let \(\mathcal{X}\) and \(\mathcal{Y}\) be the Lawvere metric spaces (i.e. Costcategories) defined by the following weighted graphs.
The product can be represented by the following graph:
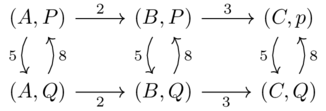
The distance between any two points \((x,y),(x',y')\) is given by the sum \(d_X(x,x)+d_Y(y,y)\).
We can also consider the Cost-categories as matrices
\(\mathcal{X}\) A B C A 0 2 5 B \(\infty\) 0 3 C \(\infty\) \(\infty\) 0 \(\mathcal{Y}\) P Q P 0 5 Q 8 0 \(\mathcal{X}\times\mathcal{Y}\) (A,P) (B,P) (C,P) (A,Q) (B,Q) (C,Q) (A,P) 0 2 5 5 7 10 (B,P) \(\infty\) 0 3 \(\infty\) 5 8 (C,P) \(\infty\) \(\infty\) 0 \(\infty\) \(\infty\) 5 (A,Q) 8 10 13 0 2 5 (B,Q) \(\infty\) 8 11 \(\infty\) 0 3 (C,Q) \(\infty\) \(\infty\) 8 \(\infty\) \(\infty\) 0 Can view this as a 2x2 grid of 3x3 blocks: each is a \(\mathcal{X}\) matrix shifted by \(\mathcal{Y}\).